Prove that the equation $x^3y^3z^33xyz=1$ defines a surface of revolution and find the analytical equation of its axis of revolution I think that I need to apply Euler's formula, so that I g Stack Exchange Network x³ y³ z³ 3xyz = (x y z) (x² y² z² – xy – yz– zx) In order to find the formula of x³ y³ z³, we need to send 3xyz to the right side of equal sign Thus the formula becomes, x³ y³ z³ = (x y z) (x² y² z² – xy – yz– zx) 3xyzIf x y z = 6, x2 y2 z2 = 16 and x3 y3 z3 = 196 Then find the value of 3xyz 1 160 2 140 3 130 4 1

U Log X 3 Y 3 Z 3 3xyz X Y Z Ux Uy Uz
X^3+y^3+z^3-3xyz formula
X^3+y^3+z^3-3xyz formula-Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchangeयदि x y z = 9, xy yz zx = 23, तब `x^(3) y^(3) z^(3) 3xyz=` A 100 B 81 C 108 D 123 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries




Vector
verify that ` x^3 y^3 z^3 3xyz = 1/2( xyz) (xy)^2 (yz)^2 (za)^2 ` Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P Bahadur IITJEE Previous Year Narendra Awasthi MS Chauhan Biology NCERT NCERT Exemplar NCERT Fingertips We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence proved Show MoreThe formula of x 3 y 3 z 3 – 3xyz is written as \(\begin{array}{l}x^{3} y^{3} z^{3} – 3xyz = (x y z) (x^{2} y^{2} z^{2} – xy – yz – zx)\end{array} \) Let
Click here👆to get an answer to your question ️ Factorise 27x^3 y^3 z^3 9xyzX 3 y 3 z 3 3xyz = (xy) 3 3x 2 y 3xy 2 z 3 3xyz = (xy) 3 z 3 3xy (xyz) = (xyz) (xy) 2 z (xy) z 2 3xy (xyz) = (xyz) (x 2 2xyy 2 xzyzz 2 3xy) = (xyz) (x 2 y 2 z 2 xyyzzx) bởi Nguyễn Thanh Huyền Like (1) Báo cáo sai phạm Cách tích điểm HP What must be subtracted from 4x^42x^36x^22x6 so that the result is exactly divisible by 2x^2x1?
Answer is (xy z)(x^2 y^2 xyz z^2) You can check by multiplying it out Notice that each term is a perfect cube x^3 y^3 = (xy)^3 So we have a sum of cubes, and the factoring formula is a^3 b^3 = (ab)(a^2abb^2) So we use a = xy and b = z to get x^3 y^3 z^3 = (xy)^3 z^3 = ((xy) z)((xy)^2(xy)zz^2) =(xy z)(x^2 y^2 xyz z^2) check by multiplying itGiven x y z = 8, xy yz zx = 15 Formula used x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz Q1 There were 1 students who went for summer camp students joind them after some time, Due to which the cost of consumption increased by Rs 80 per day and the average cost of each students decrease by RsSo,x3y3z3−3xyz =(xyz)(x2y2z2−xy−yz−zx) = (xyz)((xyz)2−3xy−3yz−3zx) = (xyz)((xyz)2−3(xyyzzx) = 9(92−3×23) = 9(81−69) = 9×12 = 108 (a) 108 Mathematics Secondary School Mathematics IX Standard IX Suggest Corrections 0




If X Y Z 0 Show That X3 Y3 Z3 3 Xyz Brainly In




Answers
Given x y z = 0 Formula used x3 y3 z3 = {(x y z) × (x2 y2 z2 xy yz zx)} 3xyz Calculation &rA With hundreds of Questions based on Algebra, we help you gain expertise on Quantitative AptitudeAll for free Explore Testbook Learn to attain the subject expertise with usX^3y^3z^33xyz=(xyz)(x^2y^2z^2xyyzzx)a^3b^3c^33abc=(abc)(a^2b^2c^2abbcca)a^3b^3c^33abc formula proofx^3y^3z^33xyz formula proofaA) 36 b) 40 c) 42 d) 48




Prove That X Y3 Y Z3 Z X3 3x Yy Zz X 2x3 Y3 Z3 3xyz Maths Polynomials Meritnation Com




Vector
Complete stepbystep answer Now, we will use partial differentiation It is denoted by ∂ We are given u = log (x3 y3 z3 3xyz) So, partially differentiating u with respect to x, we get ∂u ∂x = 3x2 3yz (x3 y3 z3 3xyz) Similarly, partially differentiating u with respect to y and z, we getAnswer by lenny460 (1073) ( Show Source ) You can put this solution on YOUR website! If ${ax by cz =1}$, then show that in general ${x^3 y^3 z^3 3xyz}$ has two stationary values ${0}$ and $\frac{1}{(a^3b^3c^33abc)}$, of




Factoring Formulas In Algebra What Are Factoring Formulas




Foliation Of The Real Projective Plane By The Family Of Elliptic Download Scientific Diagram
Given (xyz) = 9∴ (x y z)2 = 92 = 81∴ x2 y2 z2 2 × 26 = 81∴ x2 y2 z2 = 81 52 = 29Now, x3 y3 z3 3xyz= (x y z) (x2 y2 z2) (xyFind the value of x3 y3 z3 3xyz if x y z 12 and x2y2z270 Hint Here, we have to find the value of the algebraic expression We will find the value of the sum of the product of the variables by substituting the given equation in the square of the sum of the three variables' identityThere are two formula of it 1 x^3 y^3 z^3 3xyz = (xyz) (x^2y^2z^2xyyzzx) 2 x^3 y^3 z^3 3xyz = (1/2) (xyz) {xy)^2(yz)^2(zx)^2}




If X Y Z 0 Then Prove That X3 Y3 Z3 3xyz Youtube




Mathematics Ii Tranquileducation
There are two formula of it 1 x^3 y^3 z^3 3xyz = (xyz) (x^2y^2z^2 xyyzzx) (xyz)(x^2y^2z^2xyyzxz) Stepbystep explanation and plz follow meConsider (x – y – z) 2 ⇒ x 2 (y 2) (z 2) 2 x (y) 2 (y) (z) 2 (z) x ⇒ (x – y – z) 2 = x 2 y 2 z 2 – 2xy – 2xz 2yz Let us prove the above equation Consider x = 2, y = 3 and z = 4 Substitute in the above equation we get LHS = (x – y – z)X y z = 2 x 3 y 3 z 3 3xyz = 74 Formula used a 3 b 3 c 3 3abc = (a b c)/2 3(a 2 b 2 c 2) (a b c) 2 Calculation According to the formula 2/2 3(x 2 y 2 z 2) 2 2 = 74 ⇒ 3(x 2 y 2 z 2) = 74 4 ⇒ x 2 y 2 z 2 = 78/3 = 26 ∴ Required answer is 26




If X Y Z 0 Then Show That X3 Y3 Z3 3xyz If X Y Z 0 Prove That X3 Y3 Z3 3xyz Youtube




Ex 2 5 11 Factorise 27 X3 Y3 Z3 9xyz Class 9 Ex 2 5
If the polynomial k 2 x 3 − kx 2 3kx k is exactly divisible by (x3) then the positive value of k is ____If x y z = 5 and xy yz zx = 1 then Find the value of (x 3 y 3 z 3 – 3xyz) (x y z) 2 1 125 2 135 3 133 4 130X^3 (yz)^3 y^3 (zx)^3 z^3 (xy)^3




Rd Sharma Solutions For Class 7 Maths Chapter 7 Algebraic Expressions Download Free Pdf




Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo
Formula x 3 y 3 z 3 3xyz = 1/2 (x y z) (x y) 2 (y z) 2 (z x) 2 Calculation According to the question ⇒ x 3 y 3 z 3 3xyz = 1/2 × (255 256 257) × (255 256) 2 (256 257) 2 (257 255) 2 ⇒ x 3 y 3 z 3 3xyz = (1/2) × 768 × (1) 2 (1) 2 (2) 2 ⇒ x 3 y 3 z 3 3xyz = (1/2) × 768 × 1 1 4If x y z = 6 and xy yz zx = 10, then the value of x3 y3 z3 3xyz is?(xyz)^3 (x y z) (x y z) (x y z) We multiply using the FOIL Method x * x = x^2 x * y = xy x * z = xz y * x = xy



11 Factorise 27r Y 2 9xy2 3x 4 3x 5 12 Verify That X Y Z 3xyz X Y Z X Y Y 2 2 X Show That X 3 Y 3 Z 3 3mm Snapsolve




Example 32 Show That Determinant 2xyz X Y Z 3 Class 12
Answer (1 of 5) I thought I give it a try as well I have added a mirror, so the depth is easier to comprehend It is a somewhat rounded version of But although the graph seems to be a curved table cloth, there are actually three straight lines embedded these three lines are of course (z(xyz) (x ^ 2 xy y ^ 2 xzyz z ^ 2) หลักฐาน โปรดทราบว่า x = y z เป็นคำตอบของ x ^ 3y ^ 3z ^ 33xyz = 0 เสียบ x = y z ในสมการข้างต้น (y z) ^ 3y ^ 3z ^ 33 (y z) yz = y ^ 3 3y ^ 2z 3yz ^ 2 z ^ 3 y ^ 3z ^ 33y ^ 2z3yz ^ 2 = 0 เราจึงสามารถหารSolution x = 2x, y = 2y and z = 4z If x y z = 0, then x 3 y 3 z 3 = 3xyz 8x 3 27y 3 64z 3 = 3 (2x) (2y) (4z) = 48xyz After having gone through the stuff given above, we hope that the students would have understood, "x cube plus y cube plus z cube minus 3xyz" Apart from the stuff given in this section, if you need any other




Solving A Quadratic Equation By Factoring A Plus Topper




Bits Of Math Problem Cubes And Cube Roots
(xyz)^3 put xy = a (az)^3= a^3 z^3 3az ( az) = (xy)^3 z^3 3 a^2 z 3a z^2 = x^3y^3 z^3 3 x^2 y 3 x y^2 3(xy)^2 z 3(xy) z^2 =x^3 y^3 z^3 3 x^2y 3xy^2 3 ( x^2 y^2 2xy ) z 3x z^2 3yz^2 =x^3y^3z^3 3x^2 y3xy^2 3x^2 z 3y^2 z 6xyz 3xz^2 3 yz^2 arrange in orderThen we get x 3 ( x y) 3 = ( x y z) 3 − 3 x ( y z) ( x y z) By using equation (1) we can simplify the RHS of the above equation And by using equation (2), we can further expand LHS of the above equation Hence, by using equation (1) and (2), weGiven x y z = 6, x2 y2 z2 = 10 x3 y3 z3 = 12 Formula used (x y z)2 = x2 y2 z2 2(xy yz zx) x Q1 There were 1 students who went for summer camp students joind them after some time, Due to which the cost of consumption increased by Rs 80 per day and the average cost of each students decrease by Rs



X3 Y3 Z3 3xyz




New Solutions Of 1 Download Table
Show activity on this post The answer is yes, the rational points on your surface lie dense in the real topology Let's consider the projective surface S over Q given by X3 Y3 Z3 − 3XYZ − W3 = 0 It contains your surface as an open subset, so to answer your question we might as well show that S(Q) is dense in S(R)If x y z = 8, xy yz zx = 15 then find x3 y3 z3 3xyz 1 151 2 152 3 153 4 251 5 180 In this question formula a 3 b 3 c 3 3abc = (abc)(a 2 b 2 c 2 abbcca) is used LHS part (xy) 3 (yz) 3 (zx) 3 3(xy)(yz)(zx) =(xy yz zx




A Lift Coming Down Is Just About To Reach The Ground Floor Taking The Ground Floor As Origin And Positive Direction Upwards For All Quantities Which Of The Following Is Correct




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Class 9th Ex 2 5 Question 12 Youtube
Now the formula x 3 y 3 z 3 – 3xyz = (x y z) (x 2 y 2 z 2 – xy – yz – zx) Putting the given values ⇒ 80 – 3xyz = 8 × (24 – ) ⇒ 3xyz = 80 – 32 = 48 ⇒ xyz = 16 ∴ Required value of xyz = 16 Short trick Putting, x = y = 2 and z = 4Answer (1 of 2) Put x y = a, y z = b and z x = c Then a b c = x y y z z x = 0 Since a³ b³ c³ 3abc = (a b c)(a²b²c² ab bc caX 3 y 3 z 3 − 3 x y z = (x y z) (x 2 y 2 z 2 − x y − y z − x z)




Verify That X3 Y3 Z3 3xyz X Y Z 2 X Y Y Z X Z Brainly In




Find The Value Of 1 1 1 X 2 Y 2 Z 2 X 3 Y 3 Z 3
Note that (can be easily seen with rule of Sarrus)$$ eginvmatrix x & y và z \ z và x và y \ y & z & x \ endvmatrix=x^3y^3z^33xyz$$ On the other hand, it is equal to lớn (if we địa chỉ cửa hàng to the first row 2 other rows)$$ eginvmatrix xyz và xyz & xyz \ z & x và y \ y & z và x \ endvmatrix=(xyz) eginvmatrix 1 & 1 & 1 \ z và x & y \ y & z & x \ endvmatrix=(xyz




If X Y 222 And Z 223 Then Find The Value Of X 3 Y 3 Z 3 3xyz




Vector




Find The Value Of X 3 Y 3 Z 3 3xyz If X 2 Y 2 Z 2 And X Y Z 15 Youtube



2




What Is The Formula Of X3 Y3 Z3 Book Vea



What Does The Graph Of Math X 3 Y 3 Z 3 1 Math Look Like Quora




Show That X3 Y3 Z3 3xyz X Y Z X2 Y2 Chegg Com




File




Evaluate X3 Y3 Z3 3xyz When X 2 Y 1 And Z 3 Brainly In




Prove That X Y3 Y Z3 Z X3 3x Yy Zz X 2x3 Y3 Z3 3xyz Maths Polynomials Meritnation Com



2



2




Pdf On Solving The Diophantine Equation 𝑥 𝑦 𝑧 𝑘 On A Vector Computer




If X Y Z 0 Then Show That X3 Y3 Z3 3xyz




Using The Identity And Proof X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx



2




Prove That X Y 3 Y 3 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Maths Number Systems Meritnation Com



Solved 0 Given X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Chegg Com



Calculate The Unit Vector Which Is Normal To The Surface ϕ X 2y Xy 2 3xyz At The Point 1 1 1 Sarthaks Econnect Largest Online Education Community




Ex 2 5 Q No 12 Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




Polynomials Ppt Video Online Download




If X Y Z 0 Then Show That X Cube Y Cube Z Cube 3xyz Mathematics Topperlearning Com Vj2f0044



A New Version Of Ksor Method With Lower Number Of Iterations And Lower Spectral Radius Springerlink



2



Verify That X 3 Y 3 Z 3 3xyz Frac 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Snapsolve



2



Verify Euler S Theorem For The Function U X 3 Y 3 3xy 2 Sarthaks Econnect Largest Online Education Community



If X Y Z 6 And Xy Yz Zx 10 Then What Is The Solution Of X 3 Y 3 3xyz Quora



Find Div Vector F And Curl Vector F Where Vector F Grad X 3 Y 3 Z 3 3xyz Sarthaks Econnect Largest Online Education Community




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Qnababa Com




Polynomials Ppt Video Online Download



If X Z 225 And Y 226 Then What Is The Value Of X Y Z 3xyz Quora




Unit 2



Show That The Functions U X Y Z V Xy Yz Zx And W X 3 Y 3 Z 3 3xyz Are Independent And Find The Relation Between Them Mathematics




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube



3 If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz Snapsolve




Let X Be The Am And Y Z Be Two Gms Between Two Positive Numbers Then Y3 Z3 Xyz Is Equal To A 1 B 2 C 1 2 D None Of




Polynomials Ppt Video Online Download




Maths Formulas For Class 10




2 Polynomials Note Blast



Cbse 9 Math Cbse Polynomials Ncert Solutions




Rd Sharma Solutions For Class 7 Maths Chapter 7 Algebraic Expressions Download Free Pdf




Prove That X3 Y3 Z3 3xyz Half X Y Z X2 Y2 Y2 Z2 Z2 X2 Rn Maths Polynomials Meritnation Com



Nprobability Wolfram Language Documentation




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube



X2 Y2 Z2




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video




X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Proof It Lhs To Rhs Brainly In



Let X Y Z Be Positive Reals Which Of The Following Implies X Y Z I X 3 Y 3 Z 3 3xyz Sarthaks Econnect Largest Online Education Community




48 Mathematics Example 24




Cbse Class 10 Maths Formulas Geeksforgeeks




The Lfham Solution Of Kdv Equation Example 1 For A 0 99 For N 1 H Download Scientific Diagram




Pdf On Solving The Diophantine Equation 𝑥 𝑦 𝑧 𝑘 On A Vector Computer




Polynomials Ppt Video Online Download



X3 Y3 Identity




Pdf On Solving The Diophantine Equation 𝑥 𝑦 𝑧 𝑘 On A Vector Computer



2




U Log X 3 Y 3 Z 3 3xyz X Y Z Ux Uy Uz




If X Y Z 0 Show That X 3 Y 3 Z 3 3x Y Z




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5




If X 3 Y 3 Z 3 3xyz And X Y Z 0 Find The Value Of X Y 2 Xy Y Z 2 Yz Z X 2 Zx



2




Evaluate X 3 Y 3 Z 3 3xyz When X 2 Y 1 And Z 3



2
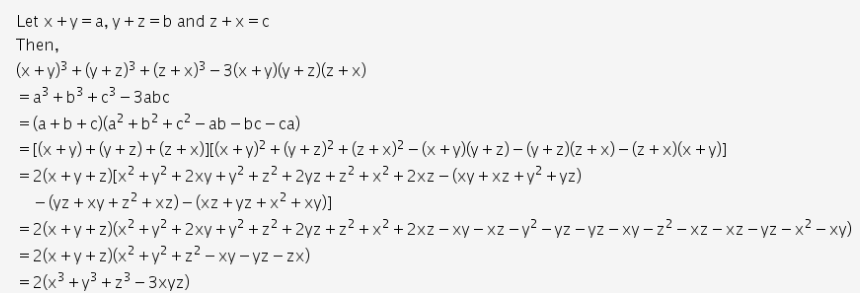



Raj Stosunkowo Poduszka X 3 Y 3 Przerazenie Uwiezienie Przed Siebie



How To Prove That Math X Y Z 3 27xyz Geq0 Math Quora
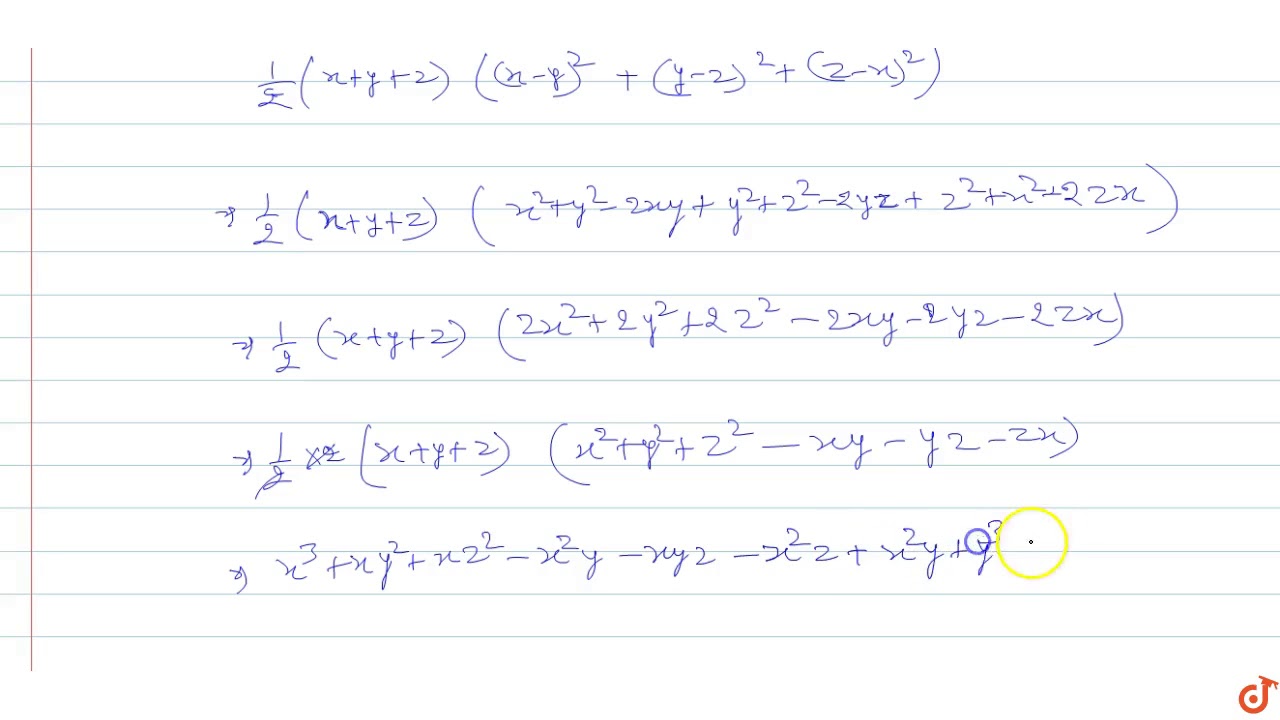



Blogerjokioqkay ベスト ƒxƒ ƒzƒ ƒn ƒaƒjƒ



2




I Need An Example For This Formula X3 Y3 Z3 3xyz Brainly In




Ex 2 5 14 Without Actually Calculating The Cubes Find The Value Of
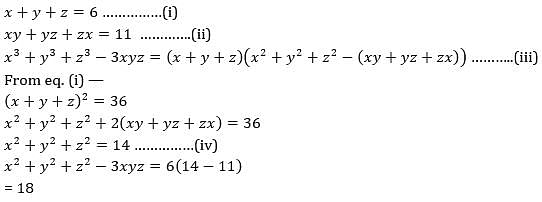



Mathematics Mock Test 4 100 Questions Mcq Test Cds Combined Defence Services Mock Test Series Defence




Top 19 X 3 Y 3 Z 3 3xyz All Formula




Mathematics Complex Numbers Session Session Objectives Ppt Download



2




If X Y Z 0 Then Show That X3 Y3 Z3 3xyz Class 8 Maths Cbse




File



3



2



Halp Mx1 Exam Tomorrow Bored Of Studies




Prove That X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Brainly In



Snapsolve




Verify That X Y Z 3xyz 1 2 X Y Z X Y Y Z Z X



0 件のコメント:
コメントを投稿