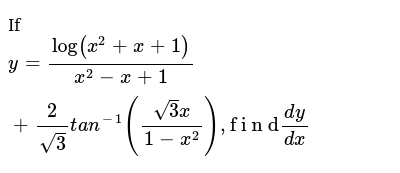
If Y Log X 2 X 1 X 2 X 1 2 Sqrt 3 T A N 1 Sqrt 3 X 1 X 2 F I N D Dy Dx
When the logarithmic function is given by f ( x) = log b ( x) The derivative of the logarithmic function is given by f ' ( x) = 1 / ( x ln ( b) ) x is the function argument b is the logarithm base ln b is the natural logarithm of b For example when f ( x) = log 2 ( x)Second derivative of sin^2;
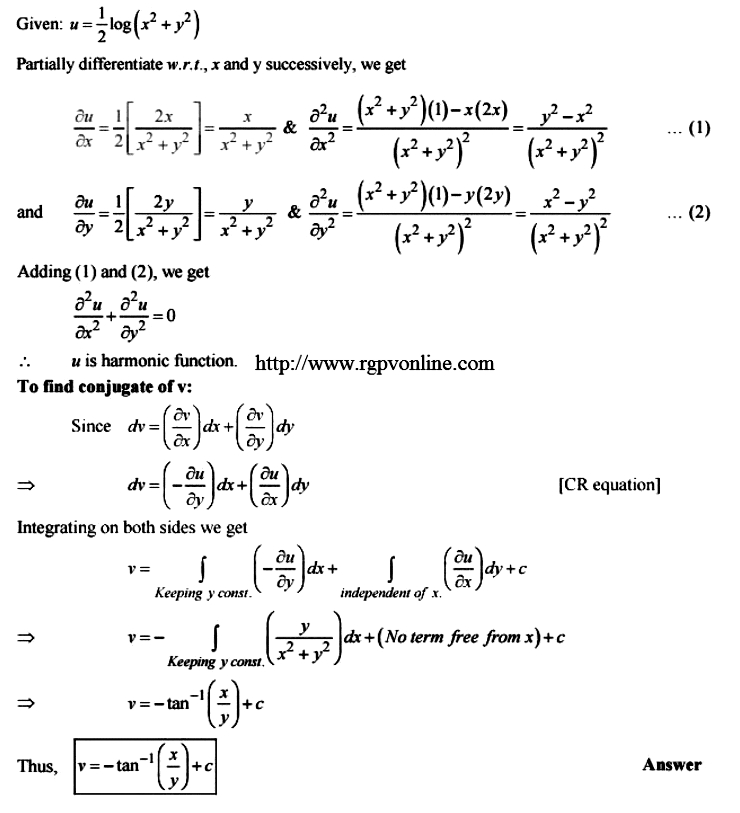
Derivative of log(x^2+y^2)
Derivative of log(x^2+y^2)- z = d d z ln z ⋅ d z d x = 1 z ⋅ d z d x This is a useful form for the logarithmic derivative of a function, sometimes written ( ln z) ′ = z ′ z ,which is worth noting in its own right for further use Now apply this with z = x x 2 y 2 so that d z d x = 1 2 x ⋅ 1 2 ⋅ 1 x 2 y 2 = x 2 y 2 x x 2 y 2 = z x 2 y 22 Write cos (x 3) as cos (x^3) 6 Ensure that the input string is as per the rules specified above An online logarithmic differentiation calculator to differentiate a function by taking a log derivative Code to add this calci to your website Just copy and paste the below code to your webpage where you want to display this calculator
Derivative Calculator With Steps
Eg1 Write sinxcosxtanx as sin(x)cos(x)tan(x) 2 Write secx*tanx as sec(x)*tan(x) 3 Write tanx/sinx as tan(x)/sin(x) 4 Use inv to specify inverse and ln to specify natural log respectively Eg1 Write sin1 x as asin(x) 2 Write ln x as ln(x) 5 Sample Inputs for Practice Eg1 Write (10x2)(x 2) as 10*x2x^2 2 Write cos(x 3) as cos Using Leibnitz theorem find the nth derivative of y= x^2( log x) Madisynstl4854 Madisynstl4854 Math Secondary School answered Using Leibnitz theorem find the nth derivative of y= x^2( log x) 2 See answers Advertisement Advertisement SkyBy SkyBy See the solution in the attached file Advertisement AdvertisementClick here👆to get an answer to your question ️ Find the second order derivatives of x^3log x Solve Study Join / Login >> Class 12 >> Maths >> Continuity and Differentiability >> Second Order Derivatives >> Find the second order deriv Question Find the second order derivatives of
Denoted by f″(x) or f(2)(x)similarly, if f" is differentialble at x , then this derivative is called the 3 rd derivative of f and it is denoted by f (3) (x) Proceeding in this way the n th derivative of f is the Get an answer for '`y = (e^x (cos(x))^2)/(x^2 x 1)` Use logarithmic differentiation to find the derivative of the function' and find homework help for other Math questions at eNotesAnd so on Here are useful rules to help you work out the derivatives of many functions (with examples below)Note the little mark ' means derivative of, and
Derivative of log(x^2+y^2)のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |
3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 | 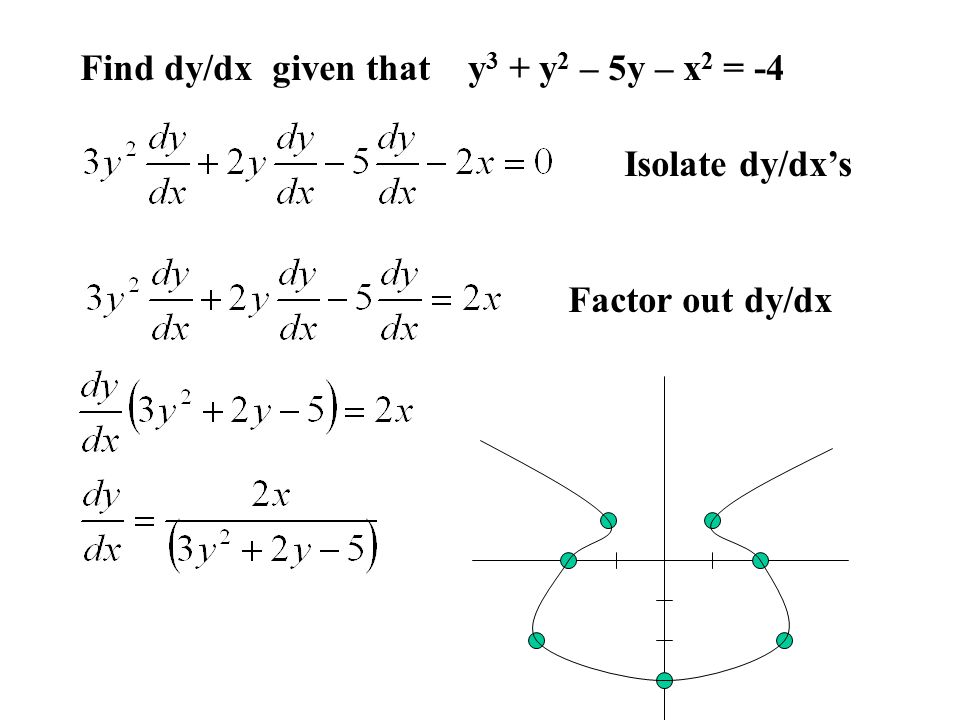 3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 | 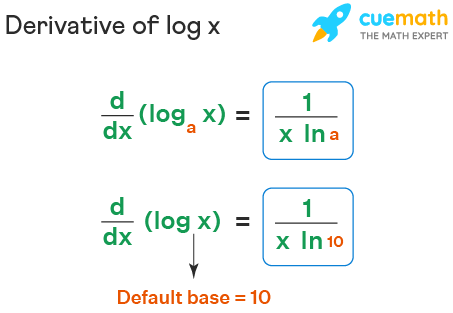 3 8 Implicit Differentiation Calculus Volume 1 | 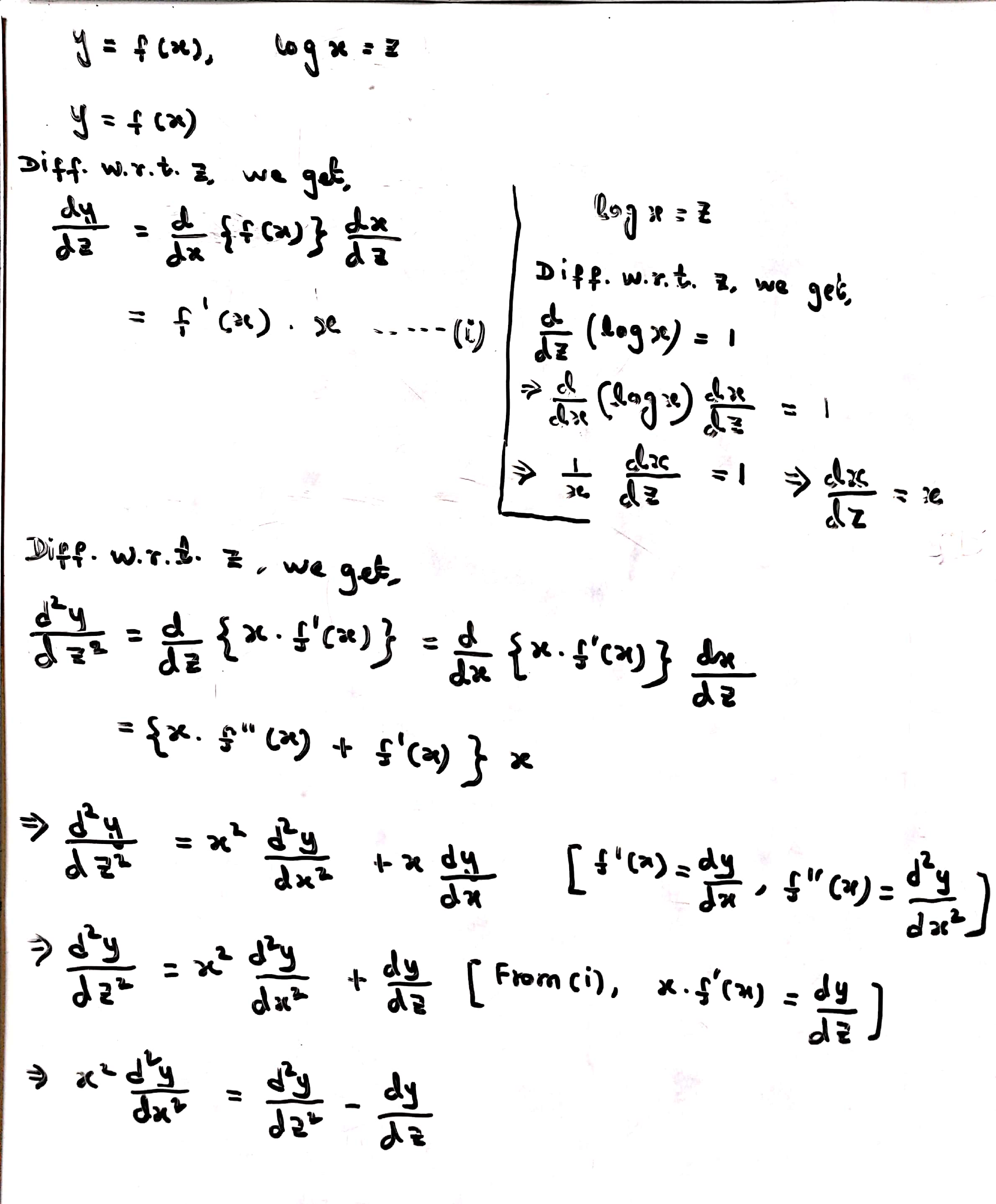 3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 | 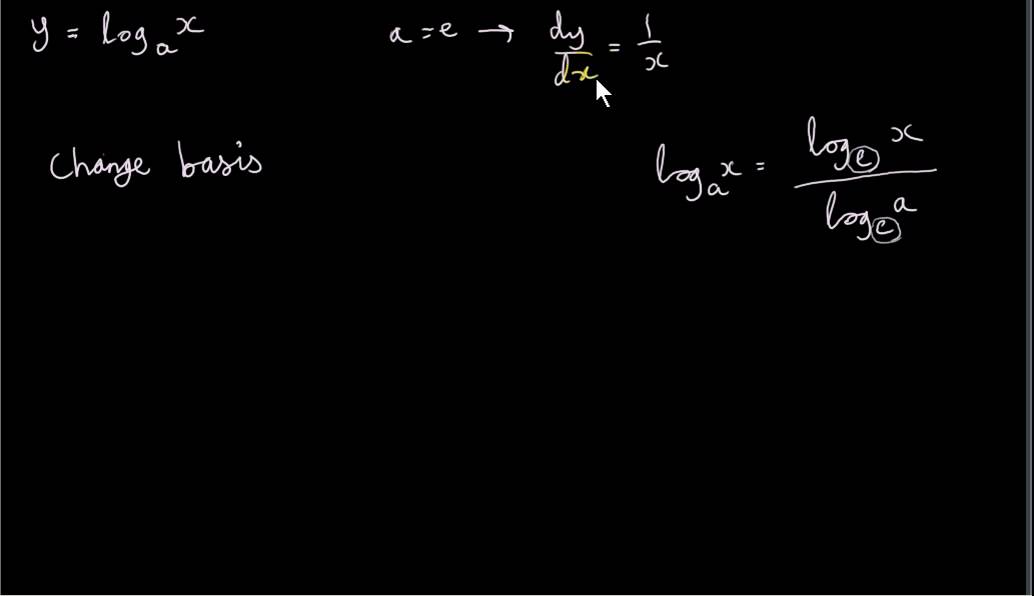 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
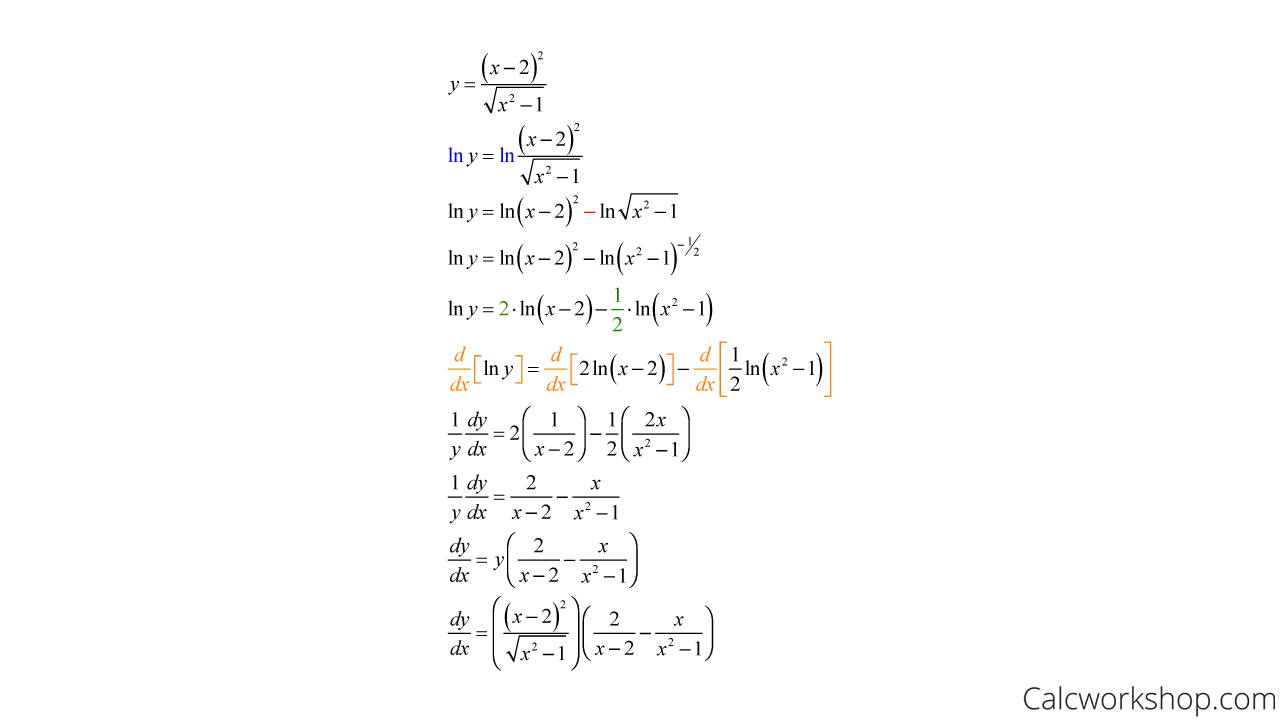 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |
3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |
3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |
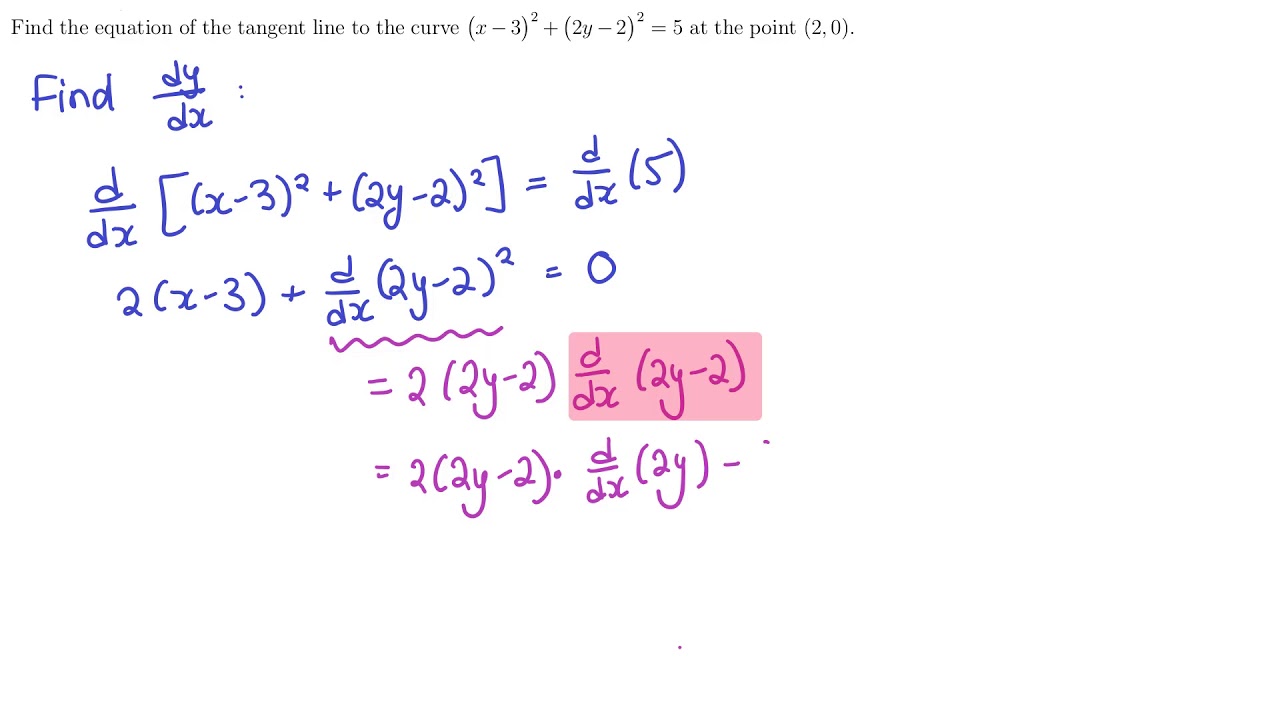 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 | 3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 | 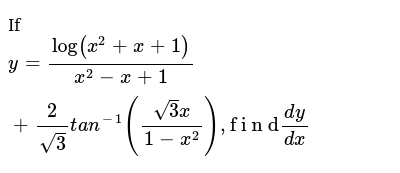 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 | 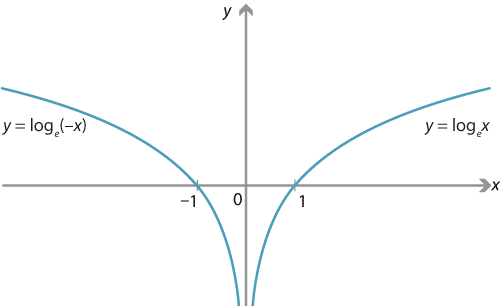 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
 3 8 Implicit Differentiation Calculus Volume 1 |  3 8 Implicit Differentiation Calculus Volume 1 |
We shall prove the formula for the derivative of the natural logarithm function using definition or the first principle method Let us suppose that the function is of the form y = f ( x) = log a x First we take the increment or small change in the function yThe derivative of the constant 2 with respect to x is 0 The derivative of the sum is the sum of the derivatives, which is 1 0 = 1 y is discontinuous at x = 0 (limit approaches 0 from the right, which is not equal to the value at 0), so the derivative does not exist at x = 0 y is undefined for x < 0 so the derivative cannot exist
Incoming Term: derivative of log(x^2+y^2), partial derivative of log(x^2+y^2),




0 件のコメント:
コメントを投稿