その2 壁に投げたボールの反射 球と球と同じくらい誰でもやりたいのが「壁と球の衝突」です。これがあると、ある入れ物の中に球を放り投げて遊ぶことができるようになります。 壁は言ってみれば平面状にずら~っとならんだ点の集まりです。そして、球であれば壁と接するのはただ1// 現在の x 軸方向の位置 const px = x (v0x * diffSecond);衝突を検知するためにボールが壁に触っている (衝突している) か確かめ、もし触っている場合には動く方向をそれに従って変更します。 計算を簡単にするために、描画される円の半径をもつ ballRadius という変数を定義しましょう。 次のコードを既にどこかにある変数定義の後に追記しましょう。 var ballRadius = 10;
モーショントゥイーンを使ってボールがバウンドするアニメーションをつくる Noralog
ボール バウンド 計算
ボール バウンド 計算-上下の板の間をボールはWの形で跳ねて行く? 上下に板をおいて板の間をバウンドするようにななめからボールを投げ入れます。 さてボールはWの文字のようにななめ上下にバウンドして進んでいくでしょうか? 上下の板を木の板、アクリル板の2種類を、ボールをピンポン玉、スーパーボールのCtxarc (px, py, r, 0, MathPI*2, false) ctxfill ();
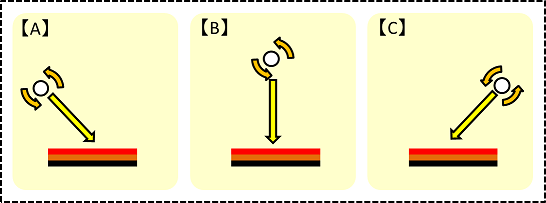


球の回転を考慮に入れた跳ね返り2 卓球の物理学 Pp Physics Com
時間計測器:1ミリ秒の正確さで計測可能な、音響的に作動するもの。 ボールを2mの高さから自由落下させ、1回目と2回目のバウンド間の時間の長さTを測 定し、以下の計算式で反発の高さH(cm)を計算する。 H=123(TΔt) 2 · ③ 計算ボール(ノーバウンドなのかワンバウンド・ツーバウンド等)を自分で選択して投げること。 このポイントを意識するだけで、守備時の送球が変わってきます。空気抵抗無く物体がある初速度と角度で打出される時の滞空時間、到達高度、到達距離を計算します。 初速度 v m/s km/h
・ ボールの回転速度(スピン)は相手コートにバウンドするまで一定である。 実際には、表計算ツールであるMicrosoft Excel のマクロを使って四次のルンゲ・クッタ法の計算手順を 組んで計算を行いました。 3 実際の問題についての試算あわせて drawBall () 関数内のボールを描画している行バウンド後の伸びが大きくなる. 初速度と打ち出し角度にも原因不明の相関があったため定量的な回転数と 伸びの関係はわからなかった. ⒉理論的なボールの運動とは異なり,打ち出し角度や初速度によっても バウンド後の伸びは変化する.
ボール作成 Visual C#でゲームを作るブロック崩し編①を解説 その1ではボールが移動し跳ね返るところまで。 基本は参考サイトを見ていただいて 初学者にわかりやすくする為、こちらでさらにコメント追記や軽い解説をしていく。T=0の瞬間に投球板の中央の上方Y 0 =180mにあるボールが,初速 でα方向に投げられたとしよう.(1)式は,ボールに水平方向速度U 0 ・COSαが初期条件として与えられるが, その後抗力係数 で表される流体力が作用して減速し,時刻tのボール位置X(t)が決まる様子を示す.(2)式は,Y方向にボール · ボール軌道の計算結果は以下のようになりました。 グラフ中の点は002秒ごとのボールの位置を表します。 カーブの方が4シームよりも3度上向きにリリースされているため、投げた瞬間は4シームよりも高い位置を通過する軌道になります。 その後徐々に下方向へ変化を始め、14mあたり



反射を計算しボールを箱へドーン トニーくんのバウンドボール Isuta イスタ 私の 好き にウソをつかない



セール S A Gear エスエーギア 野球 軟式球 野球軟式練習球a号球 1ダース S8 50 069 ウエイト サイズ バウンド公認基準 ホワイト お買い得
前回、「ボールをバウンドさせよう」では、基礎的な内容でボールの跳ね返りを実現しました。 前回の内容に加えて、今回は簡易物理シミュレーション、for文や配列を使ったボールの増殖です。 ボール同士の衝突はチャレンジできる人だけチャレンジしてみましょう! Game by ball 2 2 基礎:forこのことは数値計算でも容易に確認できますが、詳しくは ボールをより遠くまで投げるには(その2)をご覧ください。 しかし、断崖絶壁の上から海上に投げるような場合を除けばその角度のずれは無視できます。 ・θ=44度と46度では、44度の方が遠くまで飛びます。 これはボールが最高点ボール同士の衝突 ボールの中心同士の距離は分かりますよね。 d = √(x1x2)2 (y1y2)2 (z1z2)2 これが半径の二倍未満なら、その分の反発力が生じるとします。 F = k(2rd) (ここでは先ほどの粘性項は省略しています) (x1,y1,z1) (x2,y2,z2) d



トイザらス限定 ミニオンズ スーパーバウンドボール 表情6パターン 種類ランダム トイザらス



ボールの跳ね返り運動 Wikipedia
投げたボールのバウンド 常微分方程式の初期値問題の数値計算については、 利用できるものが色々ある。 数値計算は苦手のように思われている Mathematica で解いている人も少なくない。 一方で、数値計算の方法自体も学ぶに価するので、 そうしたときは、 「自分でプログラムを書いて · 先日アップした の続きで、ボールの自由落下に衝突判定を加えたバージョンになっています。 物理シミュレーションは衝突判定ができてなんぼです 衝突判定があると見た目的にもすごく面白いです。 では以下よりコードと結果を見てみましょう。 目次 目次 今回追加した部分 コードの解説ボールの衝突運動のシミュレーション このホームページで公開している グラフィックス・クラスライブラリ GLIBW32 に添付してあるサンプルソースにある key6cpp はカラーボールの衝突運動のアニ メーション・プログラムです。 ソースのコメントにあるようにボールの衝突の扱い は手抜き計算



エクセルで野球ボールの軌道計算 10月



Ec Seft Btbw バウンドテニスボール 2個入り バウンドテニス設備 バウンドテニス 球技 ハマヤラワ行
球の初速度の速度ベクトル V は次式で求めることができます. V = (V x, V y, V z) = ( V sinθ cosφ, V sinφ, V cosθ cosφ) したがって,ボールの位置ベクトル P = (P x, P y, P z) は,ボールの初期位置を Q = (Q x, Q y, Q z) とするとき,次式で求めることができます. P x = V x t Q x P y = (05 G t V y) t Q y P z = V z t Q z最近は表計算ソフトで微分方程式も解けますし、結果を簡単にグラフ表示することもできますので、 昔に比べるととてもやりやすくなりましたね。 さて、今回、以下のようなテーマで解析を行う計画をしています。まだ完成していない 解析もありますが、おいおい時間を見つけてアップしたい · 無限回バウンドでの総距離、時間物理の力学の問題です。問題高さ\(h\) から反発係数\(e\) の床にボールを落とした時、ボールの総移動距離、所要時間はそれぞれいくら?(\(e\neq 1\)) (adsbygoogle = w



ボールをバウンドさせたい Physic Material ロバメモ 素人のunity覚書と奮闘記



メディシング メディスン 安い ウェイトボール トレーニング 腹筋 アウトレット品 トレーニングマニュアル付き 5kg 非バウンドタイプ グロング Grong メディシンボール
スポーツボールの流体力学 福岡工業大学工学部知能機械工学科 溝 田 武 人 1.はじめに 硬式野球ボールとゴルフボールの3次元飛翔軌道解析を行っている.これらのボールは,速度や回転数,回転軸の方向などさまざまな条件で飛翔しているが,その条件をtv観察や実験によって詳しく調べるR団したっぱ ボールバウンド 前々から思っていたのですが ポケモンgoはゲットするときポケモンが攻撃してきてボールをはじくようになりますよね そこで「ずっとうまくポケモンの上で弾み続けたらゲットできるのだろうか?」と気になっていました そし · const diffSecond = (nowgetTime () init_timegetTime ()) * 001;



反発係数の公式と求め方をイラスト付きで丁寧に解説 物理が苦手な人も必見 高校生向け受験応援メディア 受験のミカタ


完売 バウンドクッション 東急スポーツオアシス メーカー公式 超目玉 Www Muslimaidusa Org
CtxfillStyle = 'rgb (63, 81, 181)';Vpx1 = vx1 R!1;ボールが画面の下を越えた場合に真となります。 つまり、ball_y の中身が、456 より大きくなったら真です。 ボールのサイズは 24×24 なので、480 24 = 456 が、ボールが画面下を超えた場合の値で



跳ねるボールのシミュレーション Matlab Simulink Mathworks 日本
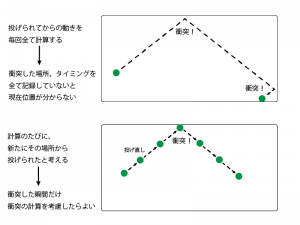


Web で物理アニメーション その4 ボールをバウンドさせよう 自主的 るぅる
てください。大きいボールがお勧めです。 バウンドの最高点の高さは,およそ次のような式で表され ます。 y = hpx ただし, グラフの例 0 y はバウンドする高さ 0 h は最初にボールを放したときの高さ 0 p はボールと床の性質によって定まる定数 0 x はバウンドの回数// 現在の y 軸方向の位置 const py = y ( (v0y * diffSecond) (05 * a * diffSecond * diffSecond)); · ということで T T T を計算します。無限等比級数の公式(→無限等比級数の収束,発散の条件と証明など)より, T = t 1 1 − e = 2 h g ⋅ 1 e 1 − e T=\dfrac{t_1}{1e}=\sqrt{\dfrac{2h}{g}}\cdot\dfrac{1e}{1e} T = 1 − e t 1 = g 2 h ⋅ 1 − e 1 e



均一なバウンドを誇る唯一の日本製卓球ボール 競技ボール 予約販売 ジャパントップトレ球 600個入り ニッタク Nb1368
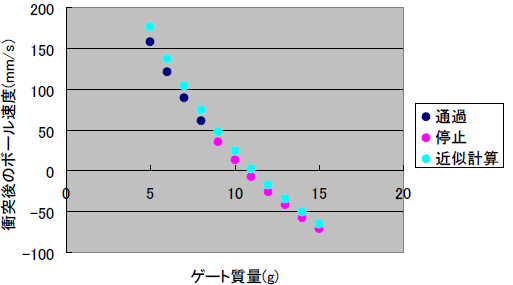


ボールの運動軌跡が簡単に計算できるの ピタゴラスイッチの計算書を作ろう 3 3 4 ページ Monoist
· バウンドゲットは複数回ボールを当てる域に到達! ポケモンの捕獲画面でボールを当てる際、当たるタイミングや位置によってはボールがバウンドすることがありますよね。 時には、 バウンドした反動でポケモンをゲットできることも!/03/18 · リバウンドボールでポケモンをゲット! 「リバウンドボール」とは、 ポケモンにボールを当て、ボールがバウンドした反動で2回目に当たったときにボールに入ってもらうという 捕獲方法です。 わかった方もよくわからない方も、まずはこちらの動画をご覧ください。Vpy1 = vy1 (バウンド前のボールの接触点の水平(鉛直) 速度) vpx2 = vx2 R!2;



ボール練習 バウンドボールを手を叩いて捕る Keita Koyamaのブログ
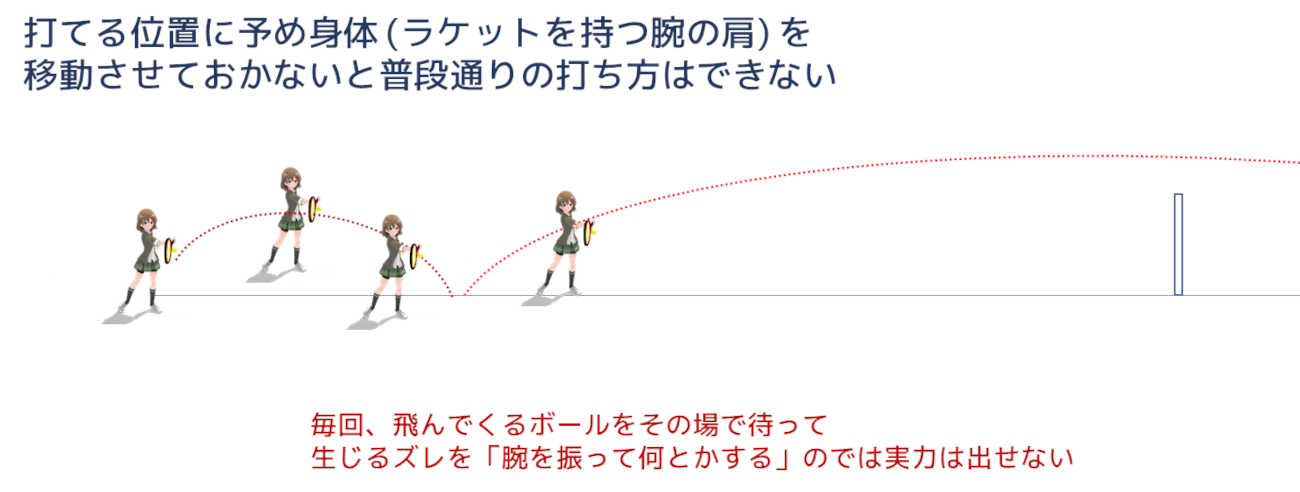


上達したい ハーフバウンド ライジング打ちがどう意味も持つのかという話 テニス Lond日記
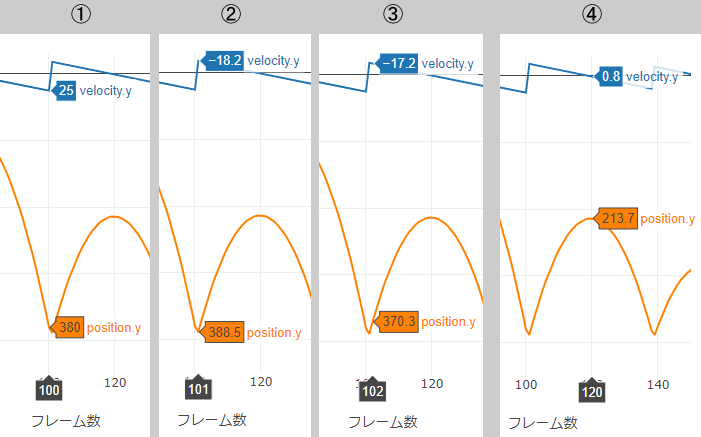
図2 バウンド時のボールの遀動のモデル化 ボールの遀動のモデル化を行ったとともに、上記(22 の記事参照)の下線邪に関して作成したモデルに合わせて 考察を行った。 ①よりθo (反射角)が小さいということが、②より予想 していた場所よりも後ろに打点をとらせること、つまり vi (入射速度 · チュートリアルをいくつか見たのですが、まだ自分には難しいです。ボールを地面に落として、バウンドさせるにはどうしたらよいでしょうか?上方へのベクタを適用するにはどうしたらよいでしょうか? Asked by SoundGuyChris 英文スレッド Product Version Not Selected s more 0 total comments;Vpy2 = vy2 (バウンド後のボールの接触点の水平(鉛直) 速度) と表す。このときボールの接触点での回転による速度は水平方向のみなので、接触点の鉛 直速度は重心と等しい。 24 バウンドの概要
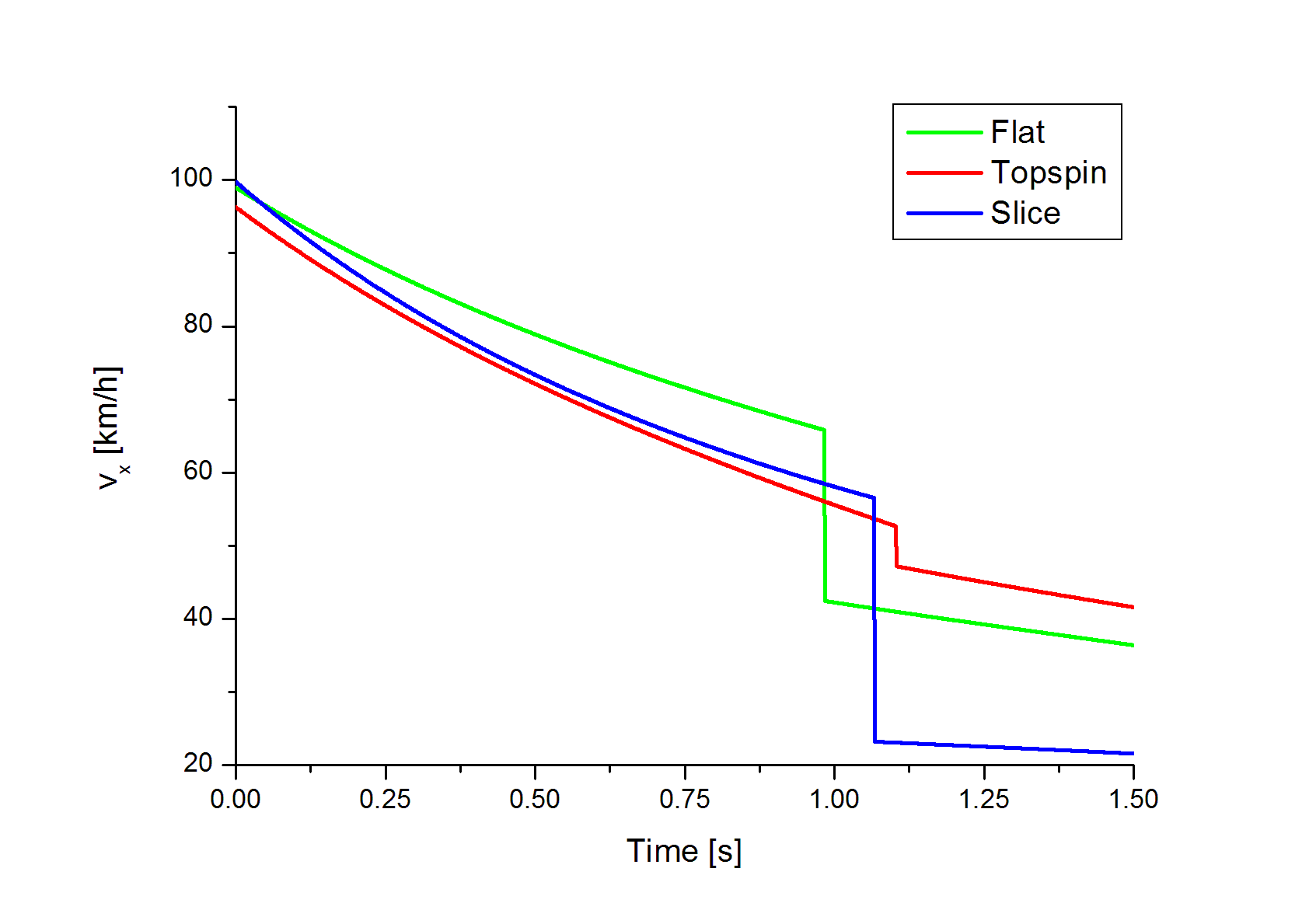


テニスの物理学 ボール軌道のシミュレーション Swingin In The Free World



均一なバウンドを誇る唯一の日本製卓球ボール 競技ボール プラ ジャパントップトレ球 Nb1367 週末限定タイムセール ニッタク 1個
· 質問バウンドボールで捕獲された方います? こんにちわ! 昨日フィールドリサーチをするために公園でポッポなどと戯れていました。 適当に投げたボールを威嚇で弾かれたのですがボールが真


モーショントゥイーンを使ってボールがバウンドするアニメーションをつくる Noralog



無限回バウンド 衝突 理系ノート



Amazon 蓄光バウンドボールが作れる おもちゃ バウンドボール製作キット おもちゃ雑貨 おもちゃ
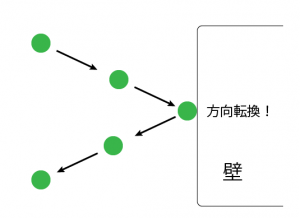


Web で物理アニメーション その4 ボールをバウンドさせよう 自主的 るぅる


ボールの衝突運動 1



Josyori Ipsj情報処理カタログ 用語集 シミュレーション



Amazon Co Jp Kicko バウンシーボール 詰め合わせ 50個 ハイバウンススーパーボール ノベルティとギャグのおもちゃ パーティーの記念品 バッグの中身 高バウンドボール おもちゃ



均一なバウンドを誇る唯一の日本製卓球ボール 競技ボール 予約販売 ジャパントップトレ球 600個入り ニッタク Nb1368
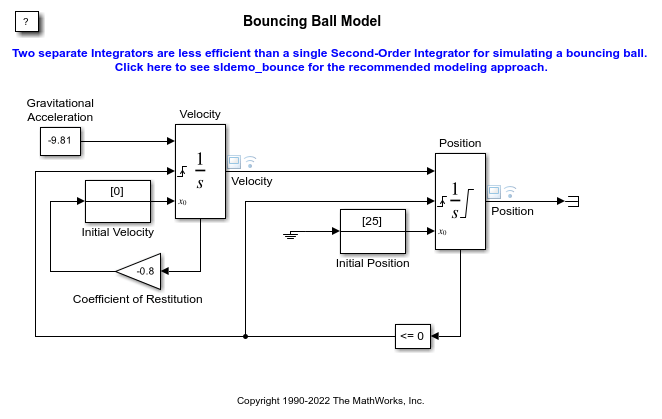


跳ねるボールのシミュレーション Matlab Simulink Mathworks 日本



第44回 宮食行次 ゴールボール 戦術的バウンドボール 東京パラリンピック Nhk



2つの力 物理学と弾性衝突への応用
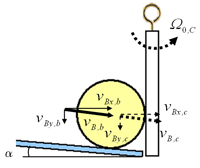


ボールの運動軌跡が簡単に計算できるの ピタゴラスイッチの計算書を作ろう 3 3 4 ページ Monoist



反発係数の公式と求め方をイラスト付きで丁寧に解説 物理が苦手な人も必見 高校生向け受験応援メディア 受験のミカタ
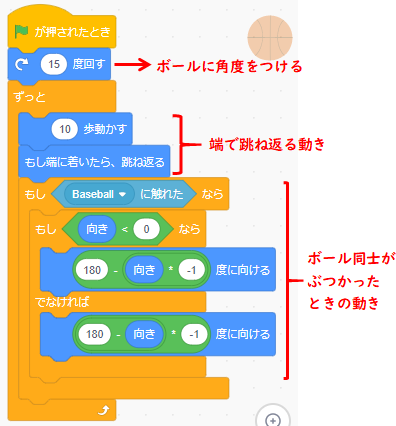


スクラッチでボールが跳ね返るプログラムの見本



Unity Physic Material 跳ね返り Bounce の設定
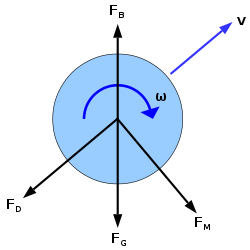


ボールの跳ね返り運動 Wikipedia
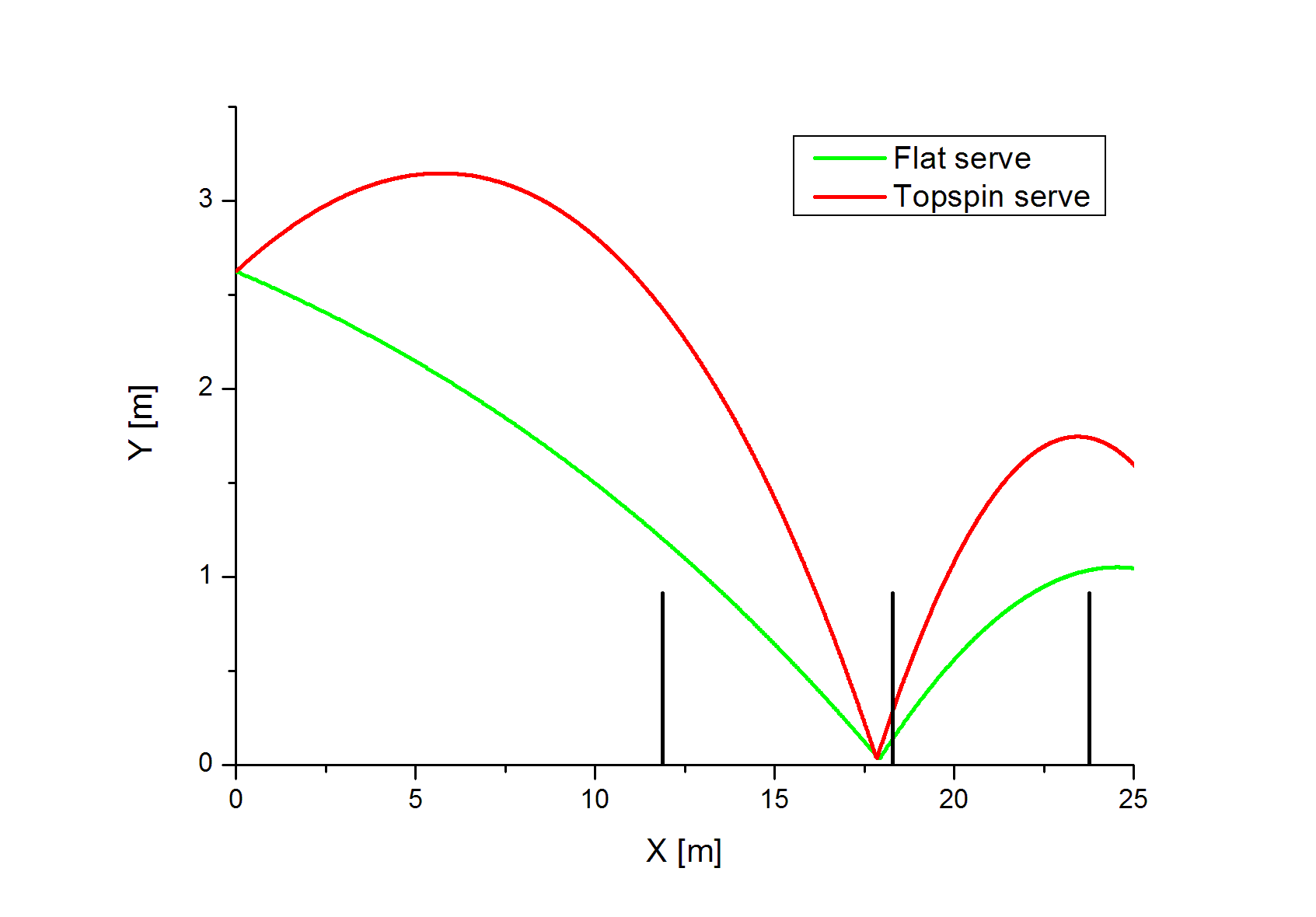


テニスの物理学 ボール軌道のシミュレーション Swingin In The Free World



Ndsolveのeventlocatorメソッド Wolfram言語ドキュメント


3ds Max のチュートリアル Massfx によるリジットボディの物理
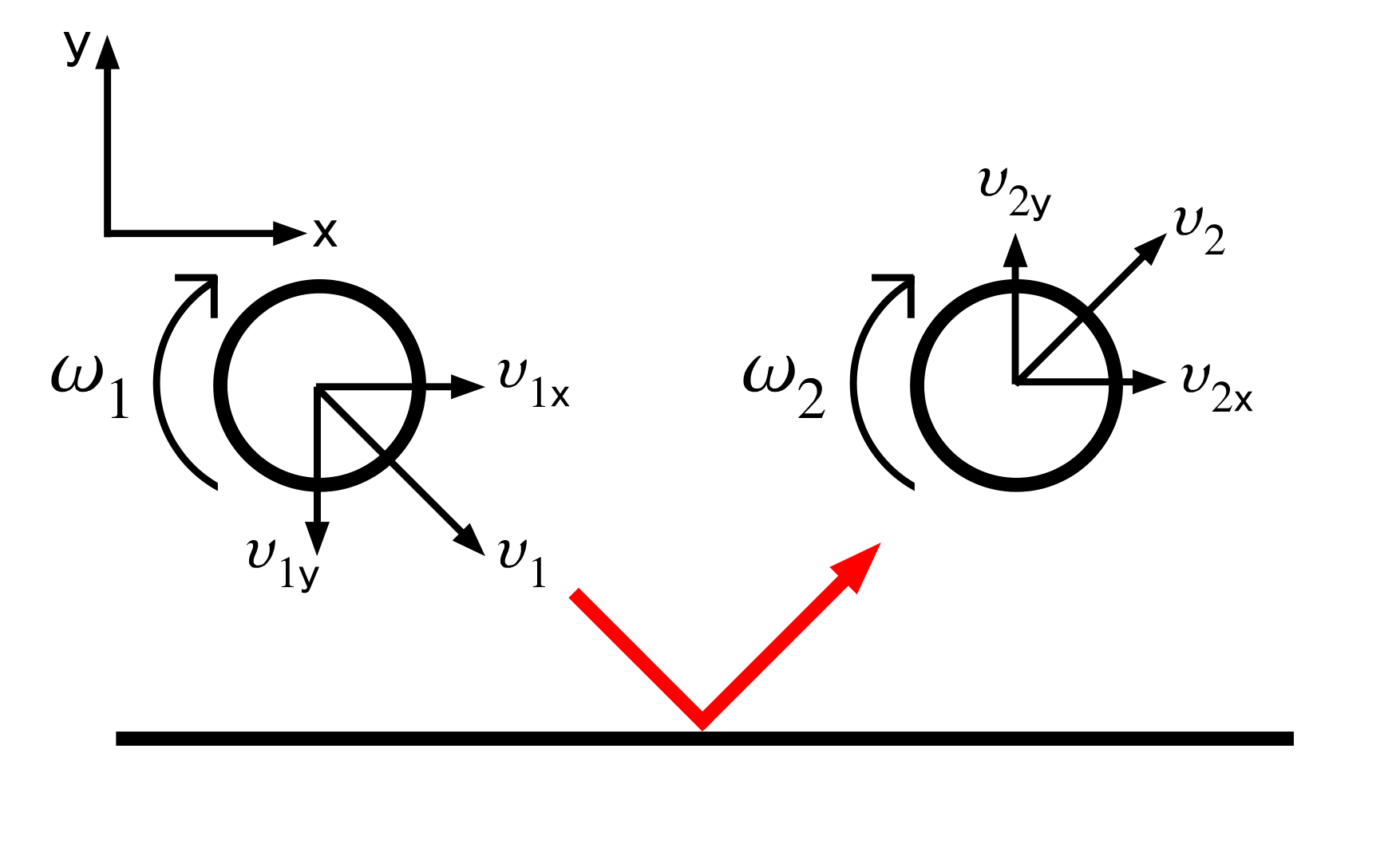


Swingin In The Free World 13年08月



反発係数を考慮した自由落下の有名問題 高校数学の美しい物語



跳ねるボールキャラアクション バウンドクエスト ひといきゲーム 無料ブラウザゲーム フラッシュゲーム



テニスの予測コツ ボールの弾み方を徹底解説 テニスやろうよ


ドロップショット 短いボールが追えない 拾えない 届かない テニス Lond日記
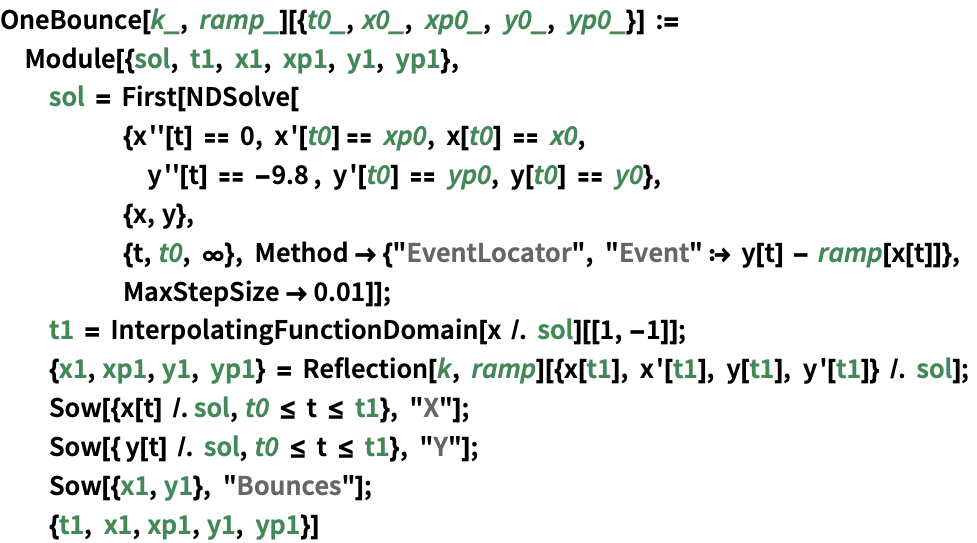


Ndsolveのeventlocatorメソッド Wolfram言語ドキュメント



作成実習6 高校物理シミュレーション


取寄品 祭り用衣類 景品 景品 子供 Kishis Eセット Eセット 縁日すくい スーパーバウンドボール Pw s パーティワールド



Amazon Ms 0 バウンドボール アクションゲーム アクションゲーム おもちゃ


7 2 P5 Play スプライトの跳ね返り Him Co ヒム カンパニー



Web で物理アニメーション その4 ボールをバウンドさせよう 自主的 るぅる
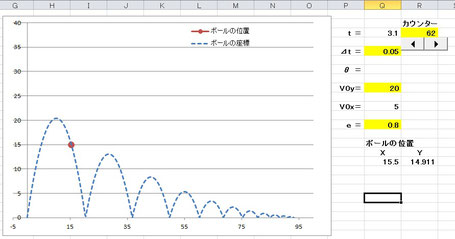


作成実習6 高校物理シミュレーション



反発係数を考慮した自由落下の有名問題 高校数学の美しい物語
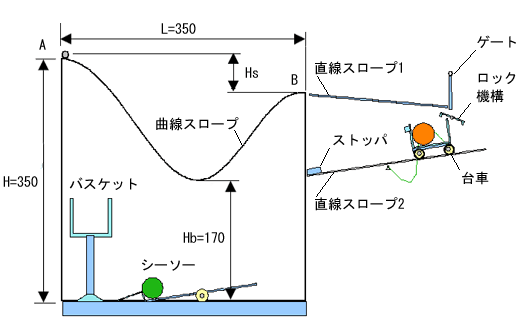


ボールの運動軌跡が簡単に計算できるの ピタゴラスイッチの計算書を作ろう 3 1 4 ページ Monoist
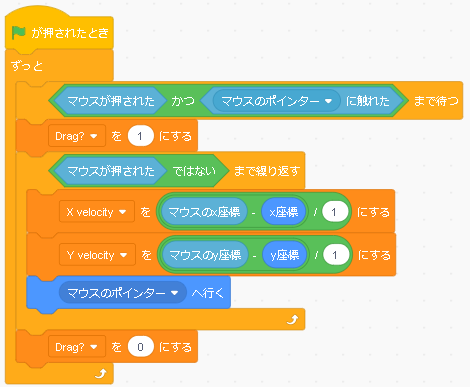


Scratch コード解析で学ぶ ボールの落下 跳ね返りを物理的に演算する Stemship



バウンス 送料込 オフ Cbj 日本語版 ボール ワンバウンド マテル テーブルゲーム バウンスオフ 陣取りゲーム パーティーゲーム



ボールのショットアクション バウンド再起動 ひといきゲーム 無料ブラウザゲーム フラッシュゲーム



エクセルで野球ボールの軌道計算 第7回 カーブ フォークボールの軌道計算



反射を計算しボールを箱へドーン トニーくんのバウンドボール Isuta イスタ 私の 好き にウソをつかない



Web で物理アニメーション その4 ボールをバウンドさせよう 自主的 るぅる


このv Tグラフはボールのバウンドの様子です そこで質問ですが なぜ赤の Yahoo 知恵袋



バウンドボールのトラップ シェアトレ サッカーの練習動画が満載



ボールバウンド発射系パズル カラークラッシュ ひといきゲーム 無料ブラウザゲーム フラッシュゲーム



球の回転を考慮に入れた跳ね返り2 卓球の物理学 Pp Physics Com



バウンドボールアクションゲーム スーパーバウンドボール ひといきゲーム 無料ブラウザゲーム フラッシュゲーム



ボール投げの最適角度は45度ではない 理系ノート



ポケモンgo バウンドゲットは複数回ボールを当てる域に到達


B 3 投げたボールのバウンド


取寄品 祭り用衣類 景品 景品 子供 Kishis Eセット Eセット 縁日すくい スーパーバウンドボール Pw s パーティワールド
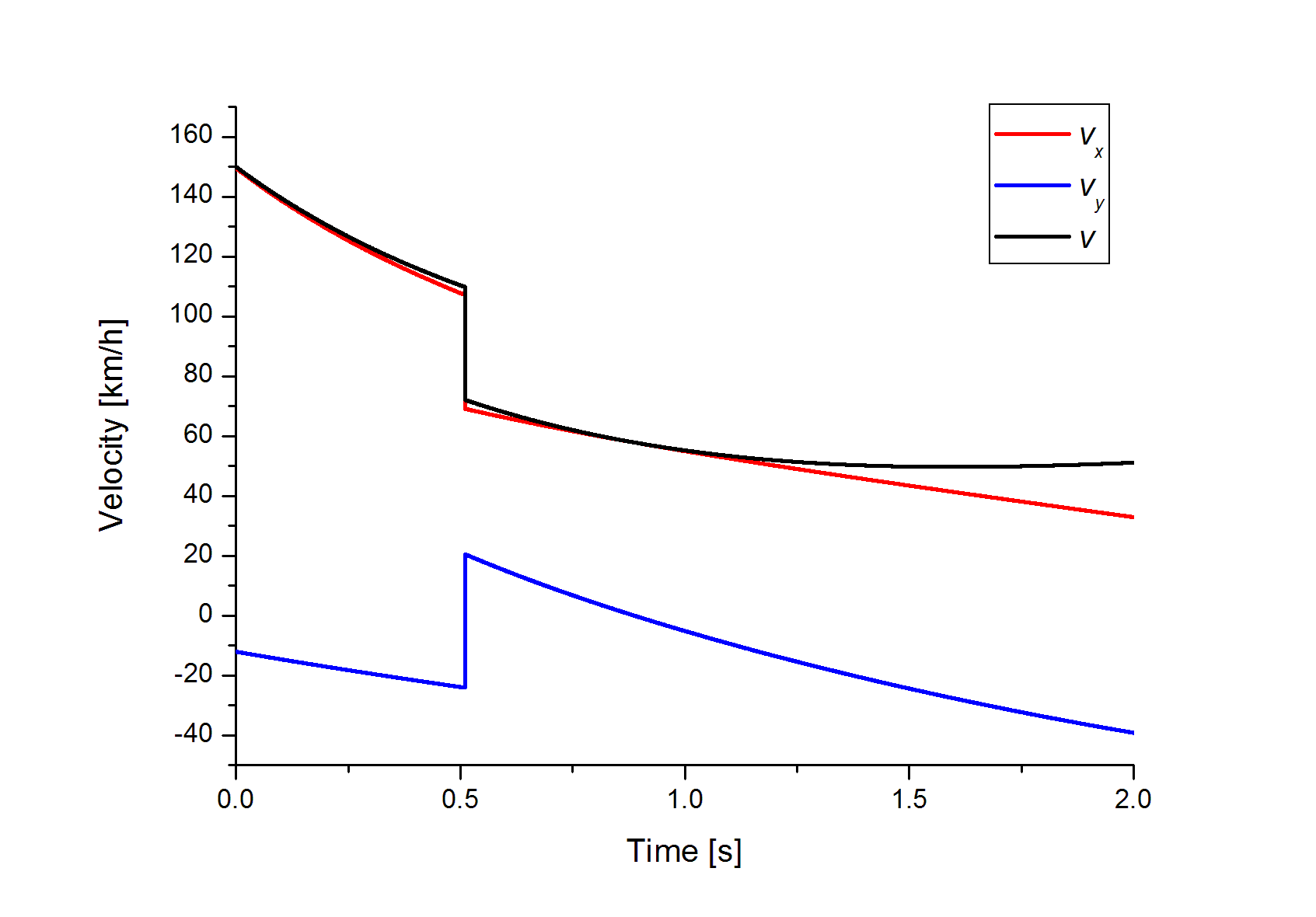


テニスの物理学 ボール軌道のシミュレーション Swingin In The Free World


取寄品 祭り用衣類 景品 景品 子供 Kishis Eセット Eセット 縁日すくい スーパーバウンドボール Pw s パーティワールド
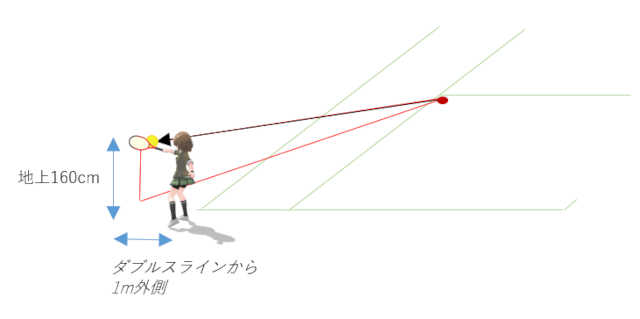


片手打ちバックハンドが苦手な高い打点 高さの違いを計算してみる テニス Lond日記



跳ねるボールのシミュレーション Matlab Simulink Mathworks 日本
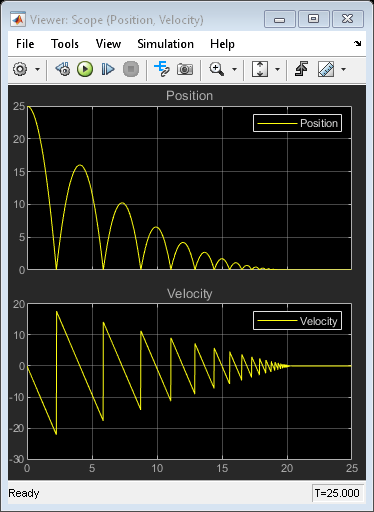


跳ねるボールのシミュレーション Matlab Simulink Mathworks 日本
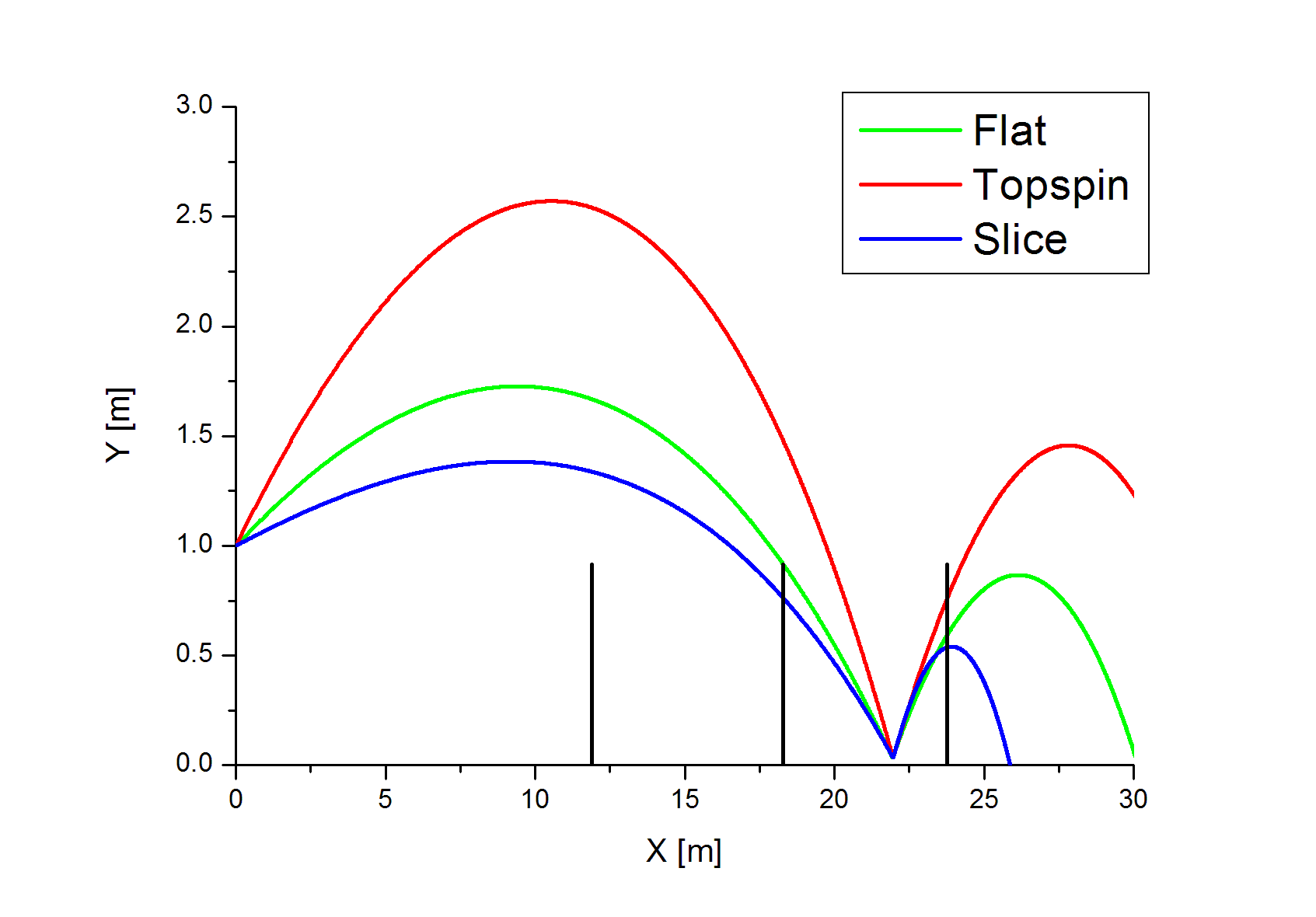


テニスの物理学 ボール軌道のシミュレーション Swingin In The Free World



作成実習6 高校物理シミュレーション
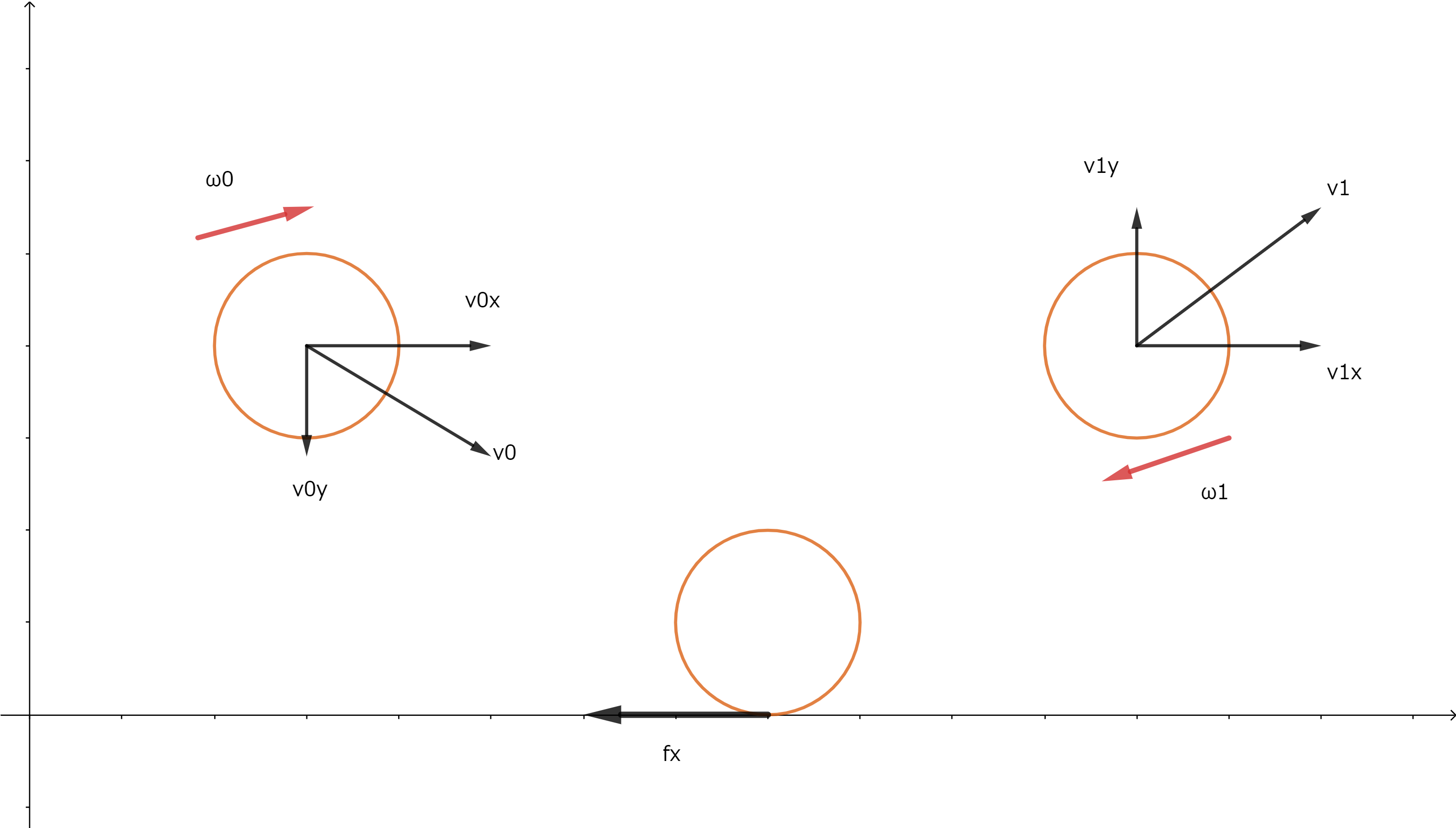


スーパーボールの運動 理系ノート



作成実習6 高校物理シミュレーション



バウンドボールのアクションゲーム バウンシングボール ひといきゲーム 無料ブラウザゲーム フラッシュゲーム
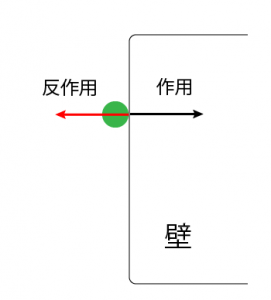


Web で物理アニメーション その4 ボールをバウンドさせよう 自主的 るぅる



ボールが1cm甘くなると 具体的にどれくらいヤバいのか 計算してみた 卓球のための数学 卓球哲学者 星名勇太 Note



Amazon Guangqi 1pcs手首バンドボール スポンジゴム高バウンドボール伸縮文字列スポーツを手首ストラップトレーニング カラーランダム ベビー用ボール おもちゃ



特別支援教育教材カタログ



阪急電車で日能研の理科の問題 スーパーボールを1mの高さから落として何回もバウンドする 勝手に難しく考えて運動方程式と反発係数で とか頭で解いてた そんな必要全くなかった Fallen Physicist Rising Engineer



面白い程良く跳ねる無重力ボール Keyword スーパーボール アウトドア 人気の定番 レジャー バウンド ボール遊び Ball Moon ムーン ボール 国内正規品 ワボバ Waboba



エクセルで野球ボールの軌道計算 第7回 カーブ フォークボールの軌道計算



トイザらス限定 ミニオンズ スーパーバウンドボール 表情6パターン 種類ランダム トイザらス
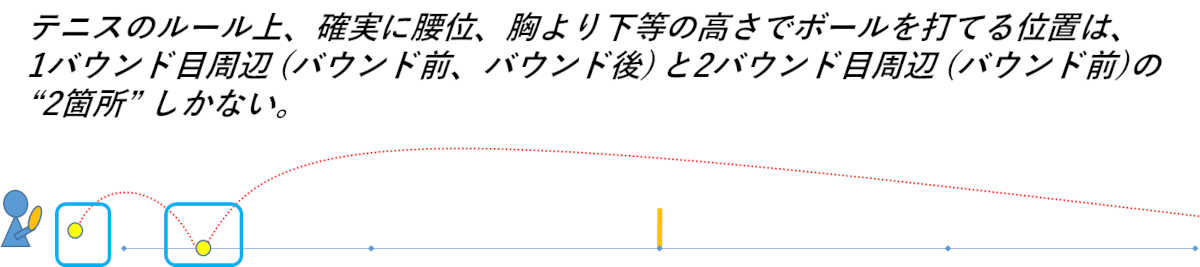


ボールを打つ際に まず 下がってしまう ことを考える テニス Lond日記



Matplotlib Animation 81 バウンドするボール サボテンパイソン
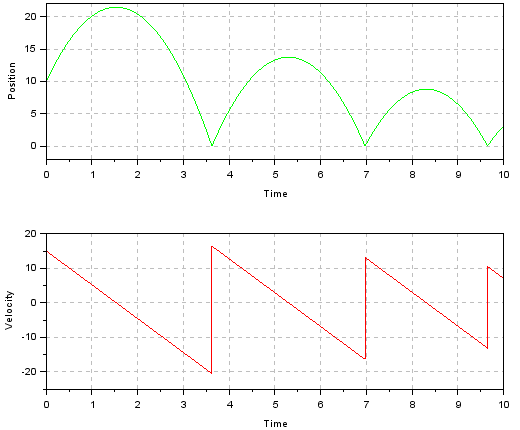


Scilabで床で跳ねるボール ねがてぃぶろぐ
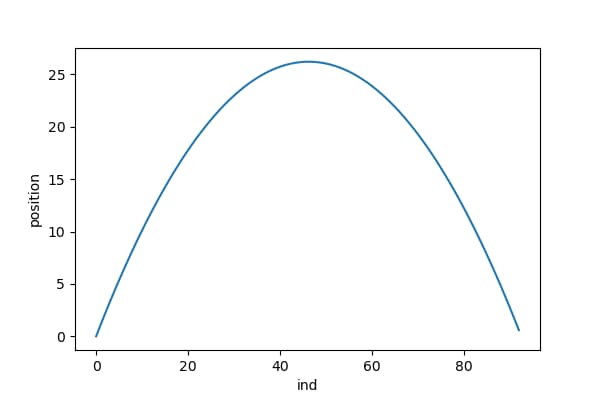


Matplotlib Animation 81 バウンドするボール サボテンパイソン



面白い程良く跳ねる無重力ボール Keyword スーパーボール アウトドア 人気の定番 レジャー バウンド ボール遊び Ball Moon ムーン ボール 国内正規品 ワボバ Waboba



バウンドボールアクションゲーム Yellow Adventure ひといきゲーム 無料ブラウザゲーム フラッシュゲーム



Web で物理アニメーション その4 ボールをバウンドさせよう 自主的 るぅる



0 件のコメント:
コメントを投稿